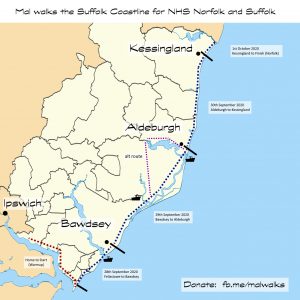
In my latest adventure I am taking on a charity walk which I devised for myself. I am walking the entire length of the Suffolk Coastline which is approx 100km.
http://fb.me/malwalks
The walk itself looks a bit like this
To support my walk I have OS Maps using Viewranger for Android, the Ordnance Survey App itself and some paper maps, but as an absolute backup I took on a small electronics project to repurpose a development board into a GPS.
Objectives
#1 Display the British National Grid reference from GPS location
#2 Display my location on a map image of some sort
Board selection
I started with what I had lying around, it needed a UART, SD card slot and a screen. So I found my EMF Camp Badge (MK3) from 2016.
SD Card Slot on the back
UART pins exposed across the top
320 x 240 colour display
D Pad and Buttons
Boot from SD card
I copied across the main scripts from the Mk3 Badge master zip file and ensured it was loading the boot and main scripts from the card, this was very easy.
WGS84 to British National Grid
Firstly I decided I should sort out converting the decimal WGS84 to BNG. I found some C code on a forum which I tested on an Arduino, then converted it to python and modified it to produce the BNG in the format i.e “TM123456”
#definitions for geometric conversions
deg2rad = 0.017453292519943295 #(PI / 180)
rad2deg = 57.29577951308232087 #(180/ PI)
a = 6377563.396 # OSGB semi-major axis
bb = 6356256.91 # OSGB semi-minor axis
e0 = 400000 # OSGB easting of false origin
n0 = -100000 # OSGB northing of false origin
f0 = 0.9996012717 # OSGB scale factor on central meridian
e2 = 0.0066705397616 # OSGB eccentricity squared
lam0 = -0.034906585039886591 # OSGB false east
phi0 = 0.85521133347722145 # OSGB false north
af0 = 6375020.48098897069 #(a * f0)
bf0 = 6353722.49048791244 #(b * f0)
n = 0.0016732202503250876 #(af0 - bf0) / (af0 + bf0)
WGS84_AXIS = 6378137 # a
WGS84_ECCENTRIC = 0.00669438037928458 #e
OSGB_AXIS = 6377563.396 #a2
OSGB_ECCENTRIC = 0.0066705397616 #e2
_xp = -446.448 #OSGB/Airy datums/parameters
_yp = 125.157
_zp = -542.06
xrot = -0.000000728190149026 #_xr -0.1502 (_xr / 3600) * deg2rad
yrot = -0.000001197489792340 #_yr -0.247 (_yr / 3600) * deg2rad
zrot = -0.000004082616008623 #_zr -0.8421 (_zr / 3600) * deg2rad
_sf = 0.0000204894 # s=20.4894 ppm
LETTERS = [ [ "V", "W", "X", "Y", "Z" ], [ "Q", "R", "S", "T", "U" ], [ "L", "M", "N", "O", "P" ], [ "F", "G", "H", "J", "K" ], [ "A", "B", "C", "D", "E" ] ]
def right(s, amount):
return s[-amount:]
def left(s, amount):
return s[:amount]
def Marc(phi):
return bf0 * (((1 + n + ((5 / 4) * (n * n)) + ((5 / 4) * (n * n * n))) * (phi - phi0)) - (((3 * n) + (3 * (n * n)) + ((21 / 8) * (n * n * n))) * (sin(phi - phi0)) * (cos(phi + phi0))) + ((((15 / 8) * (n * n)) + ((15 / 8) * (n * n * n))) * (sin(2 * (phi - phi0))) * (cos(2 * (phi + phi0)))) - (((35 / 24) * (n * n * n)) * (sin(3 * (phi - phi0))) * (cos(3 * (phi + phi0)))))
def LLtoNE(latConv,lonConv,heightConv):
latConv*= deg2rad # convert latitude to radians
lonConv*= deg2rad # convert longitude to radians
v = WGS84_AXIS / (sqrt(1 - (WGS84_ECCENTRIC *(sin(latConv) * sin(latConv)))))
x = (v + heightConv) * cos(latConv) * cos(lonConv)
y = (v + heightConv) * cos(latConv) * sin(lonConv)
z = ((1 - WGS84_ECCENTRIC) * v + heightConv) * sin(latConv)
# transform cartesian
hx = x + (x * _sf) - (y * zrot) + (z * yrot) + _xp
hy = (x * zrot) + y + (y * _sf) - (z * xrot) + _yp
hz = (-1 * x * yrot) + (y * xrot) + z + (z * _sf) + _zp
# Convert back to lat, lon
lonConv = atan(hy / hx)
p = sqrt((hx * hx) + (hy * hy))
latConv = atan(hz / (p * (1 - OSGB_ECCENTRIC)))
v = OSGB_AXIS / (sqrt(1 - OSGB_ECCENTRIC * (sin(latConv) * sin(latConv))))
errvalue = 1.0
lat1 = 0
while errvalue > (1/1024):
lat1 = atan((hz + OSGB_ECCENTRIC * v * sin(latConv)) / p)
errvalue = abs(lat1 - latConv)
latConv = lat1
output_airy_elevation = p / cos(latConv) - v
# Convert OSGB36/Airy into OS grid eastings and northings
# easting
slat2 = sin(latConv) * sin(latConv)
nu = af0 / (sqrt(1 - (e2 * (slat2))))
rho = (nu * (1 - e2)) / (1 - (e2 * slat2))
eta2 = (nu / rho) - 1
pp = lonConv - lam0
IV = nu * cos(latConv)
clat3 = pow(cos(latConv), 3)
tlat2 = tan(latConv) * tan(latConv)
V = (nu / 6) * clat3 * ((nu / rho) - tlat2)
clat5 = pow(cos(latConv), 5)
tlat4 = pow(tan(latConv), 4)
VI = (nu / 120) * clat5 * ((5 - (18 * tlat2)) + tlat4 + (14 * eta2) - (58 * tlat2 * eta2))
output_os_eastings = e0 + (pp * IV) + (pow(pp, 3) * V) + (pow(pp, 5) * VI)
# northing
M = Marc(latConv)
I = M + (n0)
II = (nu / 2) * sin(latConv) * cos(latConv)
III = ((nu / 24) * sin(latConv) * pow(cos(latConv), 3)) * (5 - pow(tan(latConv), 2) + (9 * eta2))
IIIA = ((nu / 720) * sin(latConv) * clat5) * (61 - (58 * tlat2) + tlat4)
output_os_northings = I + ((pp * pp) * II) + (pow(pp, 4) * III) + (pow(pp, 6) * IIIA)
#letters
xf = output_os_eastings/500000;
yf = output_os_northings/500000;
s1x = (trunc(xf)) + 2;
s1y = (trunc(yf)) + 1;
s1 = LETTERS[s1y][s1x];
xf = (output_os_eastings % 500000)/100000;
yf = (output_os_northings % 500000)/100000;
s2x = trunc(xf);
s2y = trunc(yf);
s2 = LETTERS[s2y][s2x];
output_grid = s1 + s2
output_east = right(str(trunc(output_os_eastings)), 5)
output_north = right(str(trunc(output_os_northings)), 5)
output = [output_os_eastings, output_os_northings, output_airy_elevation, output_grid, output_east, output_north,s1x,s1y,s2x,s2y]
return output
Connect a GPS
The next step was to put a real GPS on it and get a location back. I selected a ublox Neo-6M and mounted it (shoddily) to the back of the Badge. It could have been much more compact, I won’t risk changing it now with 1 week to go to the start of the walk (28/09/20). I 3d printed an antenna mount and glued the antenna to it. It is connected with some header pins, so I could change it in a future revision. I wish all these boards layed out the UART or SPI or I2C pins in the space order and spacing, because it is a bit of a pain.
I tried the default large ceramic active antenna, a small ceramic active antenna, a small passive lcb antenna, and a wifi antenna (cut down to 1/8th wavelength) and found that while they all worked, this large ceramic antenna seemed to perform the best in real world test.
Interfacing GPS
I found a python module online micropyGPS here https://github.com/inmcm/micropyGPS
I quickly ran out of RAM and had to take an axe to the module code and chop out stuff I wasn’t using (speed calculations & logging)
It was simple to interface the module, in the main loop it just reads characters from the UART and passes them into the module and prints them to the serial port (for testing the GPS)
my_gps = MicropyGPS()
my_gps.coord_format = "dd"
uart = UART(3, 9600, read_buf_len=1000)
while uart.any():
----ledg.on()
----char = chr(uart.readchar())
----my_gps.update(char) # Note the conversion to to chr, UART outputs ints normally
----output += char
----if (char == "\n"):
--------print (output, end = '')
--------output = ""
----ledg.off()
The location can be grabbed and converted
lat = float(my_gps.latitude[0])
long = float(my_gps.longitude[0])
location = LLtoNE(lat,long,0)
Interfacing the screen
Working with the screen is simple with ugfx, here are some examples I used
ugfx.area(0,0,140,20,ugfx.WHITE)
ugfx.text(3, 0, str(location[3] + "_" + location[4] + "_" + location[5]) + " ", ugfx.BLACK)
Loading maps
To meet objective #2, I loaded the SD cards with some gif files that represent each 1km square for example TM1941.gif, TM2041.gif etc and loaded up the current tile.
ugfx.display_image(0, 0, strimage)
ugfx.display_image(240, 0, strimage_east)
strimage is the path to the current 1km tile, and strimage_east, is the tile to the east of that. this is because the tiles are 240×240 pixels, but the screen is 320 wide, so I get 80 pixels of the next tile displayed as well to use the screen real estate.
Final result
Once I put some logic around all the examples above to take input from the buttons and added code to draw the battery voltage and cursor. Here is a video demo.
These maps bear some similarity to the Ordnance Surveys maps, but they are of course not, these few maps tiles shown here were digitally recreated by myself using mspaint 😀